AI: What does a machine learning algorithm do anyway?

Let's get started with our series on artificial intelligence from first principles.

To a lot of people, machine learning and artificial intelligence seems like magic. Many people think that the computer somehow becomes intelligent. And it seems that way when we use tools like ChatGPT!

In reality, machine learning algorithms are just a sequence of maths operations on numbers. In this article, we will develop an intuitive understanding of how these types of algorithms work.

Finding Patterns

The basic idea of any AI or ML algorithm is that there exists some relationship between a set of input variables and an output variable. So if we want to be able to predict the price of a house given its size in square feet, then the input variable is size and the output variable is price. (In reality there will be many more input variables, but lets go with this simple example for now)

We can imagine that there is some mathematical function that connects the input variables and output variable.

price = f(size)

At the start, this function f() is unknown. The goal of the machine learning algorithm is to find out what is this function f() is. Once we have determined the function f() then later on when we want to predict a house price, we can plug in the input variables into the function and it will return the output price.

Linear Regression

Let us see an example of this process with the simplest algorithm - Linear Regression. This algorithm assumes that the function f() is some sort of line. The basic formula for a line with one variable size is

price = w * size + b

Now depending on the values of w and b, we can get many different lines. Therefore the goal of the linear regression algorithm is to find the values of w and b such that it best maps the input variable size to the output variable price

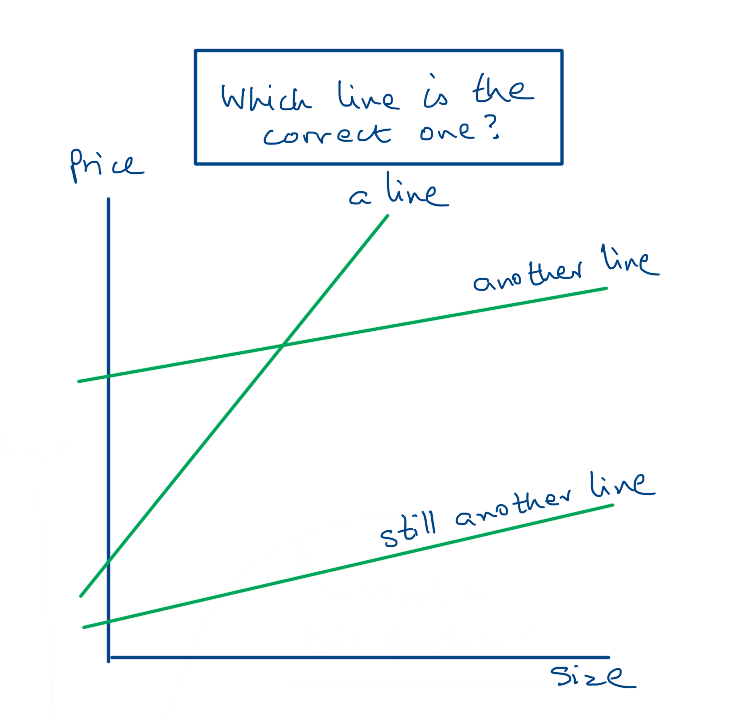
Suppose we have collected some inputs and outputs from the real world. This is our training data. We want to use this training data to determine a the values of w and b that best maps the input variables to the output.

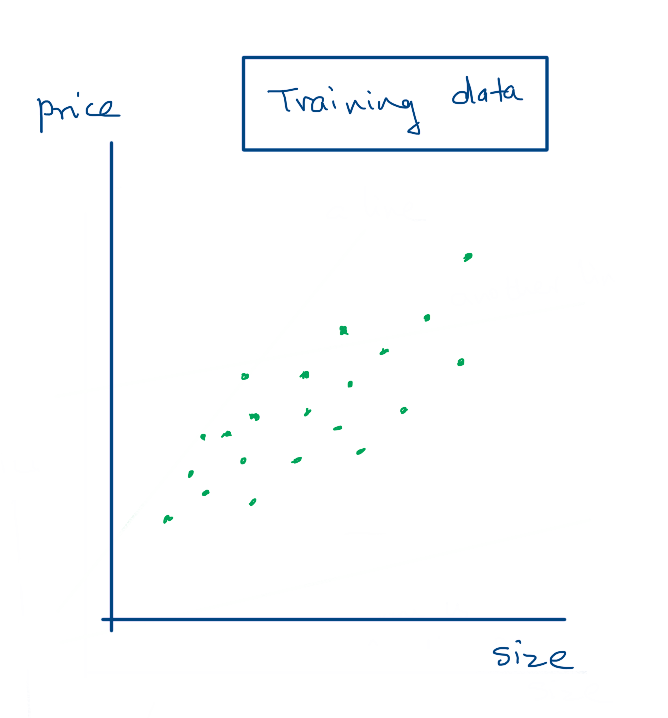
Let us start by just choosing some random values for w and b. This will give us one possible line. How good is this line? We can get a measure of that by calculating the error with the points in the training data. For a given input, what does our function predict should be the price? And what is the actual value in the training data?

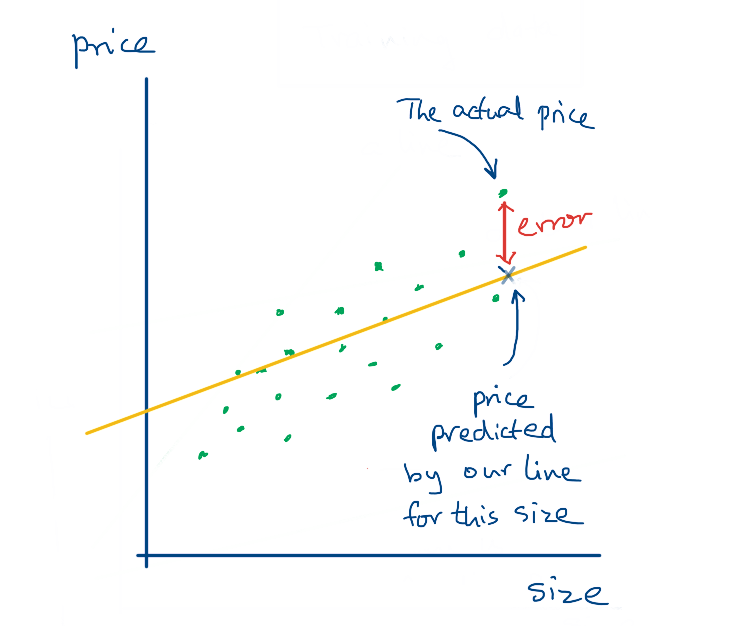
This gives us the error for a single input. We can find the error for each input and figure out the overall error of all the inputs.

Our goal here is to find the value of w and b in such a way that it minimises the error. In other words, we need to take the random w and b values that we started with and adjust them in such a way that the error will reduce.

How do we do that? This step is the core of many algorithms.

Lost in a big city

Assume you are somewhere in a big city, and you are completely lost. Worse, you don't have a map and there is no one around to ask directions. You just know where your target location is. You are at an intersection and you can see four roads leading out from the intersection. Which road do you take?

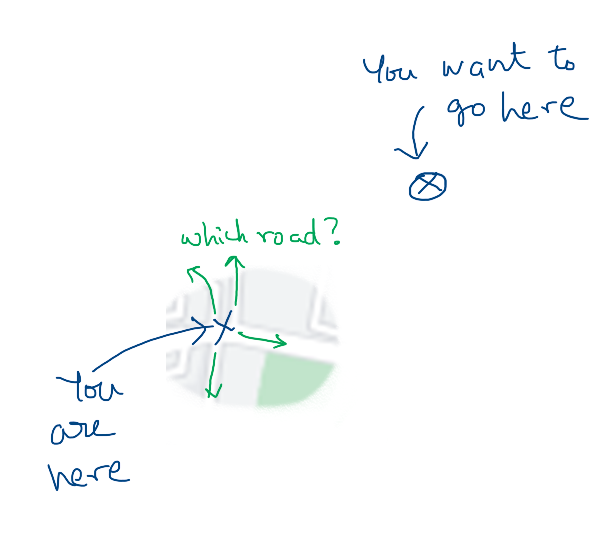
An obvious heuristic is to take the road that goes in the direction towards the target location. Now, this is not guaranteed to get you to the destination. The road you take may turn away later on, or it could be a dead end. For all you know, there may be a river and no actual path to the target, and all we can do is to get close. With the limited knowledge that we have at this point, taking the road that leads towards the target seems to be the best bet.

So we can follow an algorithm like this:

1. Look around the neighbourhood of the current location and find the paths
2. Choose the path that goes closest in the direction of the target
3. Take a few steps down that path
4. Repeat steps 1 to 3, until at some point you reach a spot where all paths take you further away
5. At this point, assume you have reached the closest that you can to the target

Now, of course, there may be another route that goes even closer to the target that we didn't find. But we don't have a map, nor the time or energy to walk all the possible paths around the city and find a shorter one. So once we come to a place where we can't get any closer, we decide to stop.

Gradient Descent

In maths, given a function f we can calculate its gradient or slope at a given point. The gradient tells us in which way the output will change if we make a tiny change to the input.

If we can determine how the error is affected by w and b, then we can use the gradient to keep changing w and b in the direction where the error will reduce.

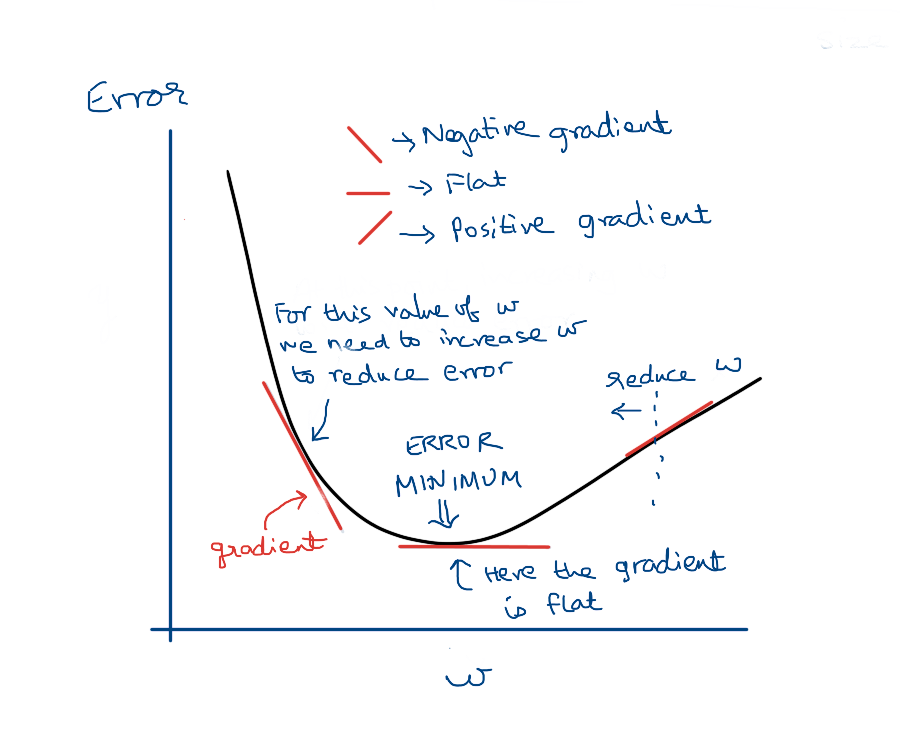
So the steps of our algorithm are:

1. Start with some random values of w and b. This will give us a function
2. Use the training data to feed inputs to this function and get the predicted output values
3. Compare the predicted outputs with the actual outputs in the training data to get the error
4. Use the gradient to adjust the values of w and b appropriately
5. Repeat steps 2 to 4 until the error doesn't seem to reduce any more

At the end of the process, we will have the values of w and b that minimises the error.

Generalising the concept

The values w and b are called the parameters of the model. These are the values, if we know them, it will determine the function. Therefore the goal of a machine learning algorithm is to find out the values of these parameters via the training data set.

Linear regression works when there is a linear relationship between the input variables and the output variables. What if the relationship is not linear? Then, no matter what values of w and b we choose, it will never map the inputs and outputs properly.

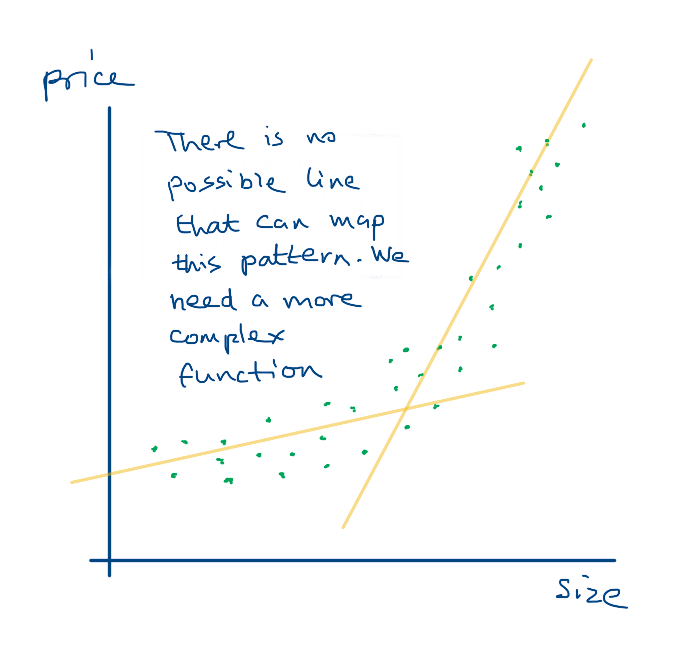
Therefore we can use more complex functions with more number of parameters, and use different error calculations. The example in this article is a two parameter model. By contrast, the LLaMa 3.1 LLM which was released by Meta this week has a really complicated function that has 405 billion parameters.

While the number of parameters is huge, the concept is still the same.

1. You have a function with some number of parameters that need to be determined
2. You have a training data set that you can use to determine these parameters. More parameters require exponentially bigger training dataset. LLMs which have billions of parameters have been trained on all the available written material that has ever been available in digital format
3. At a very high level, training process follows the steps we discussed above
   1. Start with some random values for the parameters. This gives you a function
   2. Pass in the inputs from the training data to predict the outputs
   3. Compare with the correct output and calculate the error
   4. Adjust all the parameters in such a way to reduce the error
   5. Keep repeating the process until the error doesn't reduce any more
4. At that point we have the final function which can map the input variables to the output.

Hopefully it found a function that performs well, otherwise we can try again by changing a few things. Yes, training an AI model is as much art as science 🙂

Summary

As we can see, these algorithms are essentially solving a mathematical optimisatiion problem: Using a training data set, find out the values of the parameters in such a way that the error is minimised.

In the next article in the series, we will explore a bit more into a specific kind of model called a deep learning model.