AI: Embeddings

In the previous article we saw how we can use tokenisation to convert text input into a sequence of numbers. But that's not enough! We need some way to represent meaning. Some way for the LLM to know that certain words are related.

We do that by converting the tokens from the previous stage into embeddings.

What is an embedding you ask?

Let's find out 👇🏾

Consider a math function like y = 8x + 3. When the inputs of x are similar (example, x=3 and x=3.1), the output will also be similar (around y=27). When the inputs of x are divergent (x=3 and x=100), then the output of the equation is also divergent (y=27 and y=803).

Therefore when we pass in tokens, those tokens that have similar values will result in similar outputs. If I have hello assigned to token number 1 and tiger assigned to token number 2 and I input these into the LLM, then I will get a somewhat similar output (consider that an LLM is just some sort of giant, complicated numeric function).

Wouldn't it be better if we could have words with similar meanings have similar numbers? So maybe hello could be token 1 and hi could be token 2. That would work much better.

This is a good idea, but it has a critical problem - word relationships are complicated.

For example, python and java are related words because they are both programming languages. At the same time python and cobra are related because they are both types of snakes. But java and cobra have nothing to do with each other.

The solution to this problem is to expand the number of dimensions. The diagram below shows an example of using a 2 dimensional grid - with a programming dimension and an animal dimension - to represent the words.

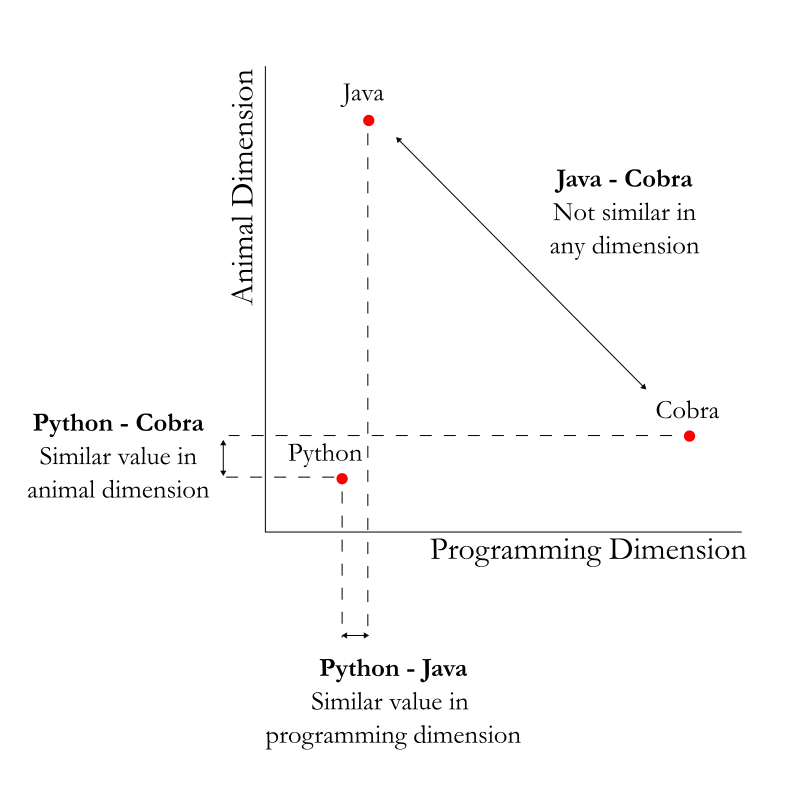
As we can see, on one axis (programming languages), we have python and java close to each other, and on the other axis (snakes) we have python and cobra close to each other. Yet, java and cobra are still far away from each other.

The example above shows two relations, but practically there are so many dimensions on which words could be related. Therefore, 2 dimensions are not enough, we need hundreds (or thousands) of dimensions.

This hundred dimension representation of a word is called an embedding.

Our problem now is to be able to convert a token into its corresponding embedding representation. There are models, called embedding models that are trained to do this mapping. These models are fed with a large corpus of data and they analyse which words appear together with which other words and find optimum embedding values for each word.

Visualising Embeddings

The diagram above shows us a visualisation of word embedding along two dimensions. How do we visualise embeddings when there are hundreds of dimensions?

One way is to project the thousand dimensions into three dimensions and display that. Of course it is not 100% accurate as projecting dimensions loses quite a bit of information. But, it is a great way to develop an intuitive understanding of an embedding.

And we can do just that at the site below 👇🏾

Embedding projector - visualization of high-dimensional data

Visualize high dimensional data.

visualization of high-dimensional dataDaniel Smilkov, Nikhil Thorat, Charles Nicholson, Big Picture

This site visualises the points from an older embedding model developed at Google called word2vec. The site projects the hundreds of dimensions into a 3D visualisation and shows the points.

You can type in a word and find out which words have a similar meaning. Here is the output when I entered the word volcano.

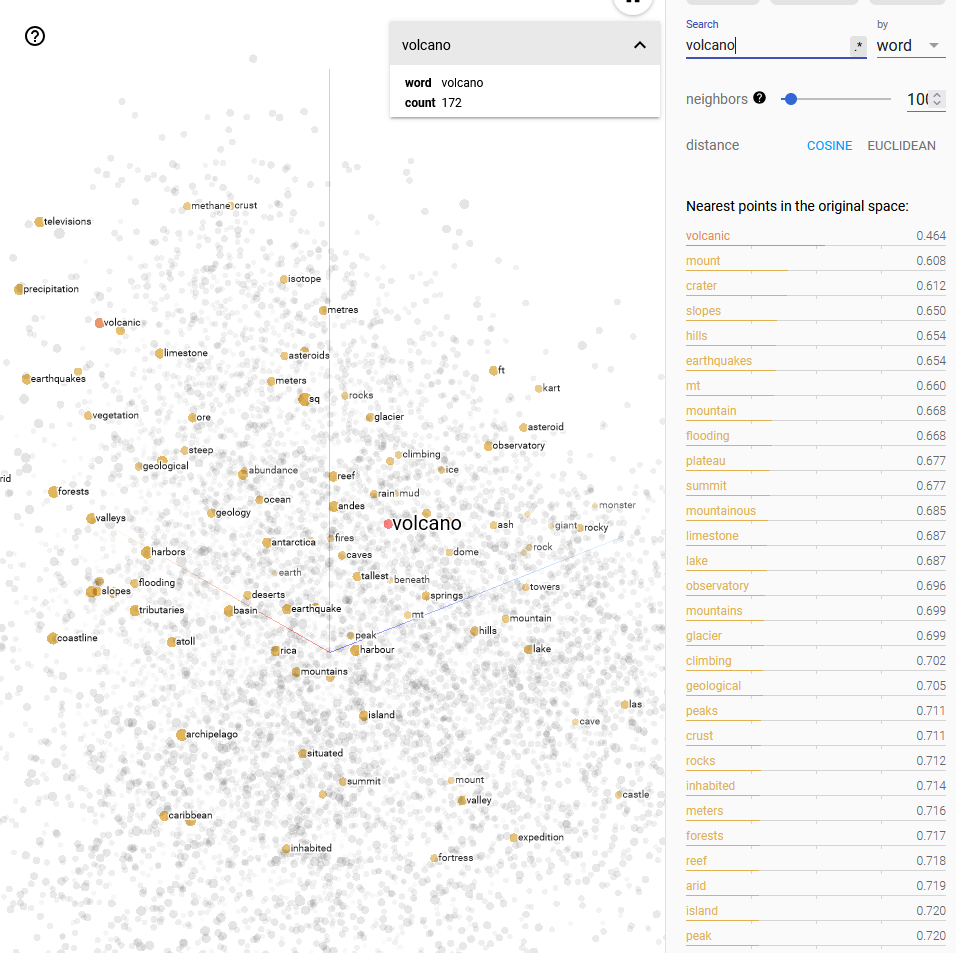
As you can see above, similar words are mount, crater, earthquakes, geological. These are words that have a similar embedding mapping to volcano.

Summary

Here is the flow we have so far:

• We get text input to the model. The tokeniser breaks down text into a sequence of numbers called tokens
• These tokens are then passed through an embedding model. The embedding model maps each token to another set of dimensions called the embedding
• These embedding numbers are what goes into the actual LLM model

Imagine a piece of text with 1000 tokens. If each token is mapped to a 4096 dimension embedding, then we will end up with 4096000 numbers which go into the LLM. You can see how the the scale of inputs balloons up rapidly.